Aki and you: How easy is the revenge actually?



Intro: Icy Tails suck … right?
Initial discussion on this episode!: Refresh Point S2 E6
Icy tails have sucked for a long time. At first glance, Aki is just a reprint of Origami from DAL set 1 with salvage and hand encore. But wait! There’s more! With the addition of easy revenge, many players have been feeling the burn (and the deckouts) that triple Aki quad easy revenge can provide.
Is a tactical decompress correct? Is Aki still just a shit finisher anyway actually? What are the actual odds that this thing will kill me?
The player base has had these few burning questions, and so did I. So, I enlisted the help of J-Man, our local mathematics doctorate, to help me make a script to run the odds of Aki killing people from any deck state with customizable parameters (number of easy revenge, number of Aki’s swinging, number of climaxes in deck and waiting room, etc. etc.) so that we could determine once and for all how dead people are, and help guide our decision making. The results may shock you. With that, the rest of this post will be written by J-Man, and by the end hopefully you’ll have some more knowledge to help you determine whether it’s REALLY worth it to try and kill that CSM player from 2.4, or try to live from 2.5 yourself.
Note: This blog post was started before Aki was heckin banned. Unfortunate. However, Scenario 3 will be pertinent to anyone still playing with/against Aki in current times. With that, please enjoy!
Part 1: The Question statement, and what Optimal Aki means
Given your gamestate, what are the odds Aki kills you? To calculate an answer to this question we break the gamestate down to the essential information that affects the probability of dealing damage and decide Aki’s logic for sequencing his actions (scry & mill, scry & leave, and icy tail). The logic used for sequencing Aki’s actions is optimal if it results in the greatest chance of victory for the Aki player.
The gamestate consists of the location of each card in your decklist. There are many zones a card may reside in, but there are only a few zones we are interested in tracking during Aki’s attack. We break down the gamestate into eight variables that are relevant for the damage cancel probability calculation: the number of cards/climaxes in the deck, cards/climaxes in the waiting room, cards/climaxes in the clock, cards in the level zone, and the bottom card of the deck. The deck is considered randomly shuffled. However, if a card at a specific position in the deck becomes known to a player this information becomes relevant for probability calculations. In Aki’s case, the bottom card of the deck may become known and hence needs to be tracked as an additional parameter. When attacking with Aki the cards and climaxes in these zones have opportunities to move to other zones. This movement of cards affects the probability of the next instance of damage sticking or canceling. For simplicity we assume the cards in a player’s hand, stage, stock, memory, and marker zones do not move zones during Aki’s attack. We also assume that a player will never voluntarily level a climax.
To introduce Aki for the unfamiliar, when Aki attacks with his climax in play he mills the bottom four cards of the opponent’s deck and burns 1 for each climax revealed. This type of mill and burn effect is commonly known as icy tail (see icy tail, Michiru). Aki also gains an additional effect for each Easy Revenge event in memory. Each copy of the event lets Aki look at the bottom card of the opponent’s deck and either leave it at the bottom or send it to the waiting room (commonly known as scry). Since the climax combo and event effects all occur when Aki attacks, you may sequence each bottom deck scry before or after the icy tail effect. After performing all the on-attack effects then Aki proceeds with the rest of the attack phase steps (most importantly the damage step). Since there is freedom in sequencing Aki’s effects this begs the question, what is the optimal way to sequence these effects and when should the Aki player leave the bottom card on the bottom of the deck?
Many players may know the answer to this question in most scenarios. Conventional wisdom is to first scry until a climax is revealed, then icy tail, then use any remaining scrys to dig for the next climax (for the benefit of another copy of Aki that has yet to attack). We will consider this logic of sequencing as “greedy”. Greedy Aki only cares about maximizing his own damage. In many common scenarios the greedy Aki logic is optimal or close to optimal. There are edge cases where trying to maximize the damage may not be the optimal play (see Appendix A for such an example). For the calculations in this article we have elected to use the logic of greedy Aki with a few simple improvements (described in Part 2B). As such, please treat these results as lower bounds on the probability of Aki’s victory.
Part 2A: How the script is constructed
We constructed a script to compute the odds of Aki dealing lethal damage. The key theory behind this script is to consider the initial gamestate as the root node of a tree. When an action is performed on this gamestate, such as dealing damage, possible outcomes are represented by children nodes. The branches connecting the root node to its children are weighted by the probability of reaching that outcome. In Weiss Schwarz every game action has a finite set of outcomes with calculable probability for each.
After a game action is performed on the root node, the next game action is performed on each child node, resulting in a new layer of children nodes. After all game actions are exhausted leaf nodes (nodes without any children) represent the final possible gamestates. The probability of reaching an individual leaf node from the root node is the product of weights along the branches on the path between the nodes.
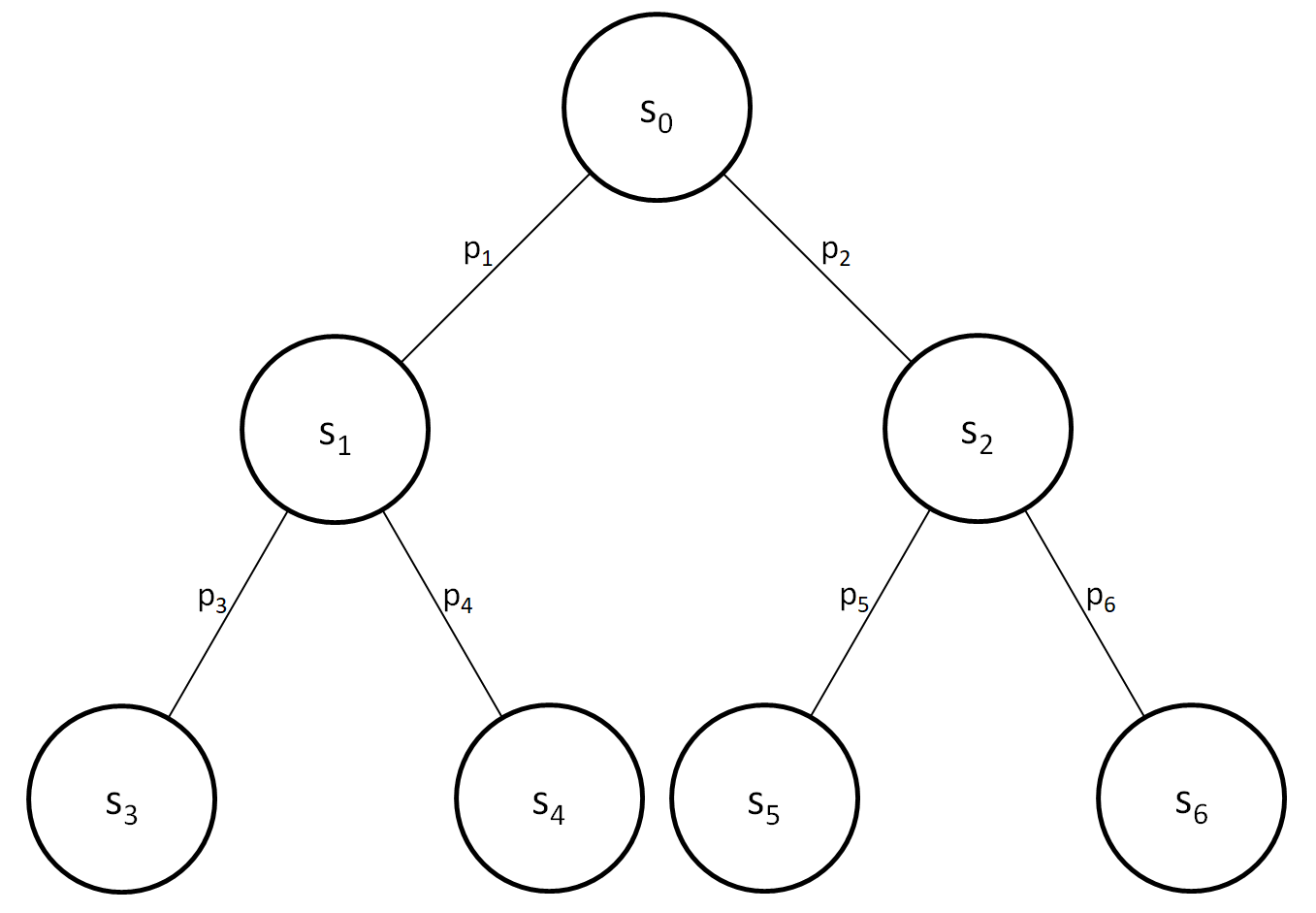
A sample tree diagram of gamestates. The initial gamestate is the root node, s0. Its children nodes, s1 and s2, have probabilities p1 and p2 of occurring respectively. Each of these child nodes has a pair of their own children nodes, resulting in four possible outcomes in total, s3, s4, s5, and s6 with probability p1p3, p1p4, p2p5, and p2p6 of occurring respectively.
From an initial gamestate we generate a tree to represent the possible resulting gamestates after three Aki attacks with combo. In particular we are interested in the leaf nodes where a player has been defeated. By summing the probability of each defeat gamestate we arrive at the odds of falling to Aki.
Part 2B: Remaining Limitations
For the calculations in the script we made some simplifying assumptions. For each attack we assume a front attack is declared and do not take into account the possibility of side attacks or any of the opponent’s effects (counters, defensive scry, etc.). These factors are very matchup dependent and do not reliably occur. We also assume we know the trigger for each attack in advance, which is not completely unreasonable given Career Advice, Aki Hayakawa.
Another assumption made is that the number of climaxes in the deck of Aki’s opponent is known by the Aki player during the attack. In actual gameplay the Aki player may be uncertain of the remaining climax count due to their opponent drawing or blind stocking cards. Knowing when the opponent’s deck has no climaxes remaining is critical for the Aki player to make optimal decisions.
As mentioned in Part 1, we used a greedy Aki algorithm to determine the sequence of on-attack effects. In general when Aki attacks, if the bottom card is unknown he will use an Easy Revenge effect to scry the bottom card, leaving it if it’s a climax or milling it if it’s a non climax. In the case of revealing and milling a non climax card, this is then followed by additional Easy Revenge bottom scrys until either a climax is revealed or all the bottom scrys have been exhausted. Next the icy tail effect is performed. After the icy tail effect, any remaining Easy Revenge bottom scrys are performed with the same logic for leaving or milling the revealed cards.
There are a few simple additional logic checks that can be performed to increase the odds of dealing damage in edge cases. One such edge case is when a deck contains zero climaxes. In this case there is no need to scry and mill non climax cards so that Aki’s soul damage will connect. Unless the deck is sufficiently small such that scrying and milling characters causes the icy tail effect to mill cards from the bottom of a refreshed deck, allowing for the opportunity to deal more damage (emphasis on greedy). Another edge case we were able to code into our algorithm is when Aki scrys after using the icy tail effect, reveals the last climax in the deck, and the deck is smaller than or equal to his soul, then it is beneficial to mill the climax so that his soul damage may connect.
No doubt there are other edge cases where unintuitive play is optimal. As is we have incorporated the edge cases we came up with into our greedy Aki algorithm to have the odds reflect close to optimal play. Please keep in mind that with good play you can slightly increase the odds shown here.
Part 3: An Exploration of The Odds
In this section we examine the odds of Aki killing a player from different initial gamestates. In particular we analyze how the odds change with respect to different parameters. From this we hope to learn what you can do as Aki’s opponent to minimize the odds of defeat. In addition to the graphical representations of the results for different scenarios, we also have included tables of the results in Appendix B.
Scenario 1A
In this scenario the Aki player has fielded three Akis with four Easy Revenge events in memory and has three blank triggers on top of their deck. We first consider a set of gamestates where Aki’s opponent is strained for resources. The total number of cards in their hand, stock, field, memory, and marker zones sums to 13 (about five hand, five stock, and three characters on the field). We keep the number of cards in the deck constant at 25 cards. This constrains the sum of cards in the level, clock, and waiting room to 12. We vary the initial level and clock from 2.0 to 3.0. This implies that the initial waiting room contains as many as ten cards (when 2.0) or as few as four cards (when 2.6). We also vary the number of climaxes remaining in the deck from four to eight. Any climaxes not in the deck are considered as starting in the waiting room.
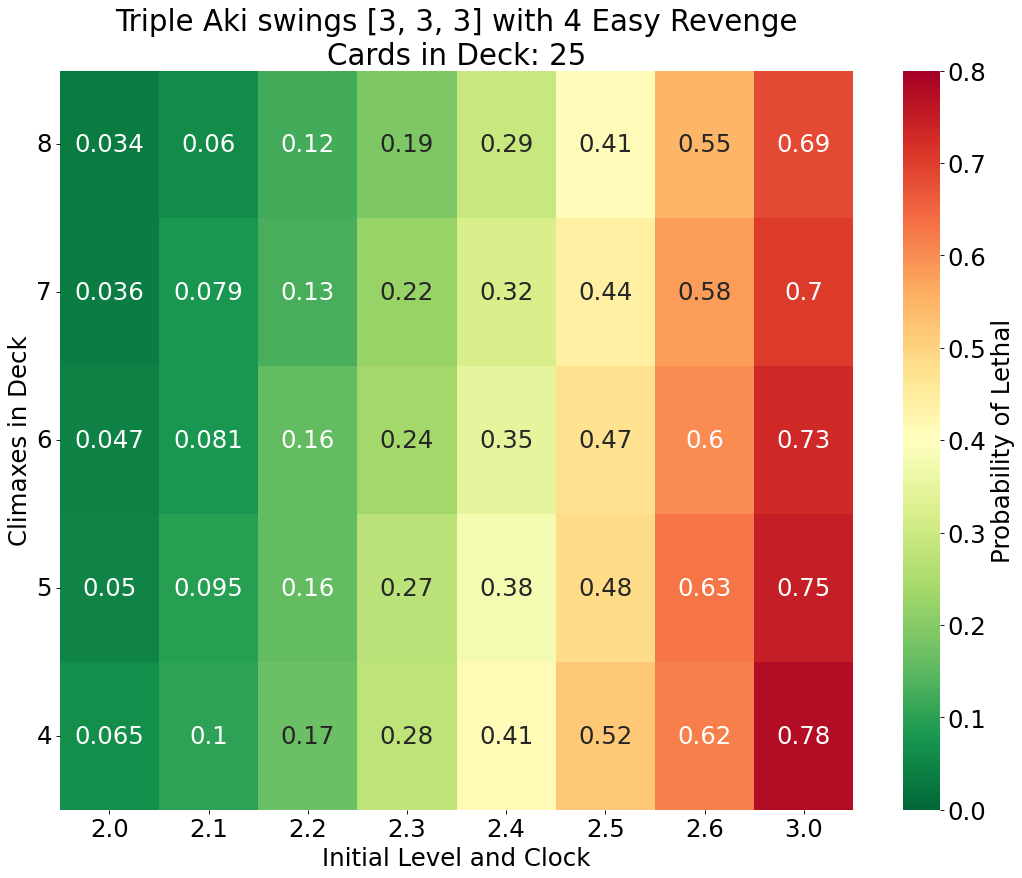
For each combination of initial level, clock, and climaxes in deck we compute the probability of triple Aki with combo landing lethal damage. From these results we can observe a common trend: as a player increases the number of climaxes in their deck, the probability of defeat decreases in general. After Aki’s release many players noted how Aki is able to punish good compression by hitting more climaxes on his icy tail effect. This observation caused players to wonder if compressing against Aki is suboptimal? Is there such a thing as a ‘tactical decompress’? These results support that a tactical decompress is rarely beneficial. The only pair of gamestates in this set that go against the general trend are for 2.6 with 4 and 5 climaxes in the deck, where the probability of lethal increases by 1% for having the additional climax in the deck.
Scenario 1B
Next we repeat the previous scenario, but suppose that Aki’s opponent is having a better game in terms of resources. For this set of gamestates the sum of cards in the hand, stock, field, memory, and marker zones is 18 (about seven hand, six stock, and five characters on the field) and the number of cards in the deck is 20. The resulting gamestates are essentially more compressed counterparts to the gamestates in Scenario 1A.
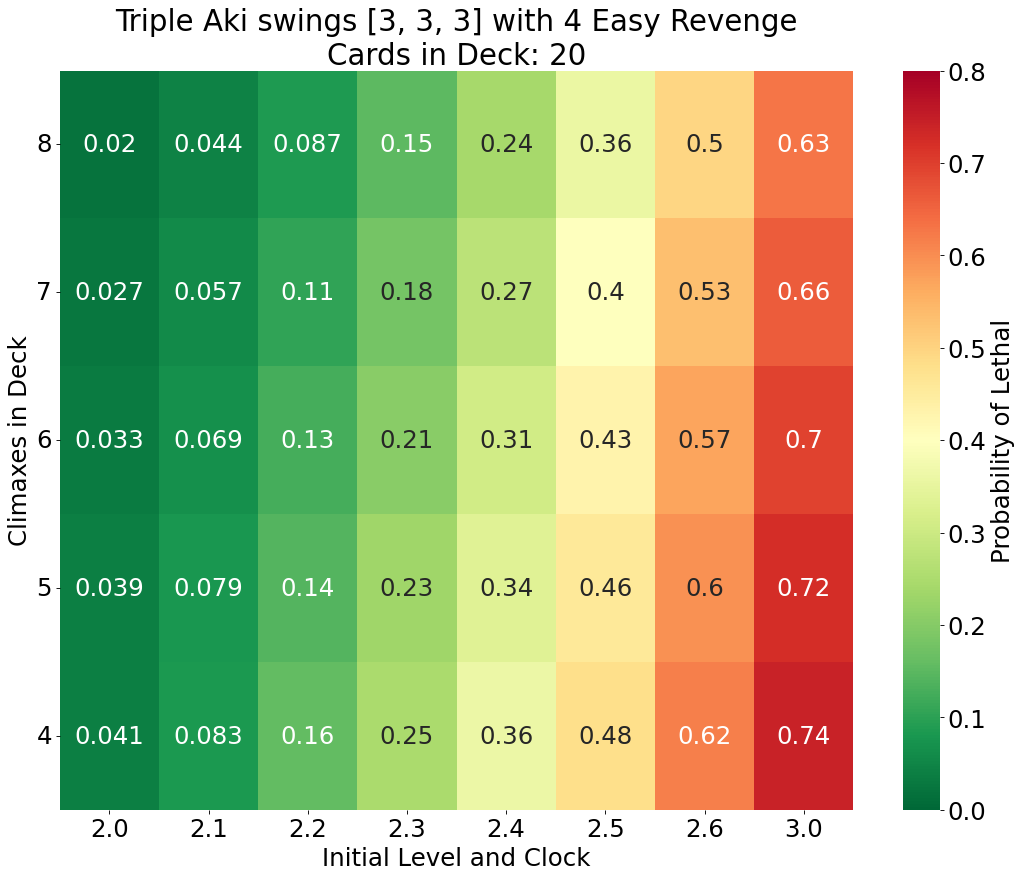
Comparing these results to those in Scenario 1A we observe that the probability of landing lethal decreases between 0.2%-5.6% and by 3.1% on average. This is additional support that compressing is a valid play against Aki.
Scenario 1C
For this scenario we consider that Aki’s opponent has been efficiently generating resources and has 23 cards between their hand, stock, field, memory, and marker zones (about seven hand, nine stock, five characters on the field, and two cards in memory). This leaves only 15 cards in the deck, resulting in some very compressed deck states.
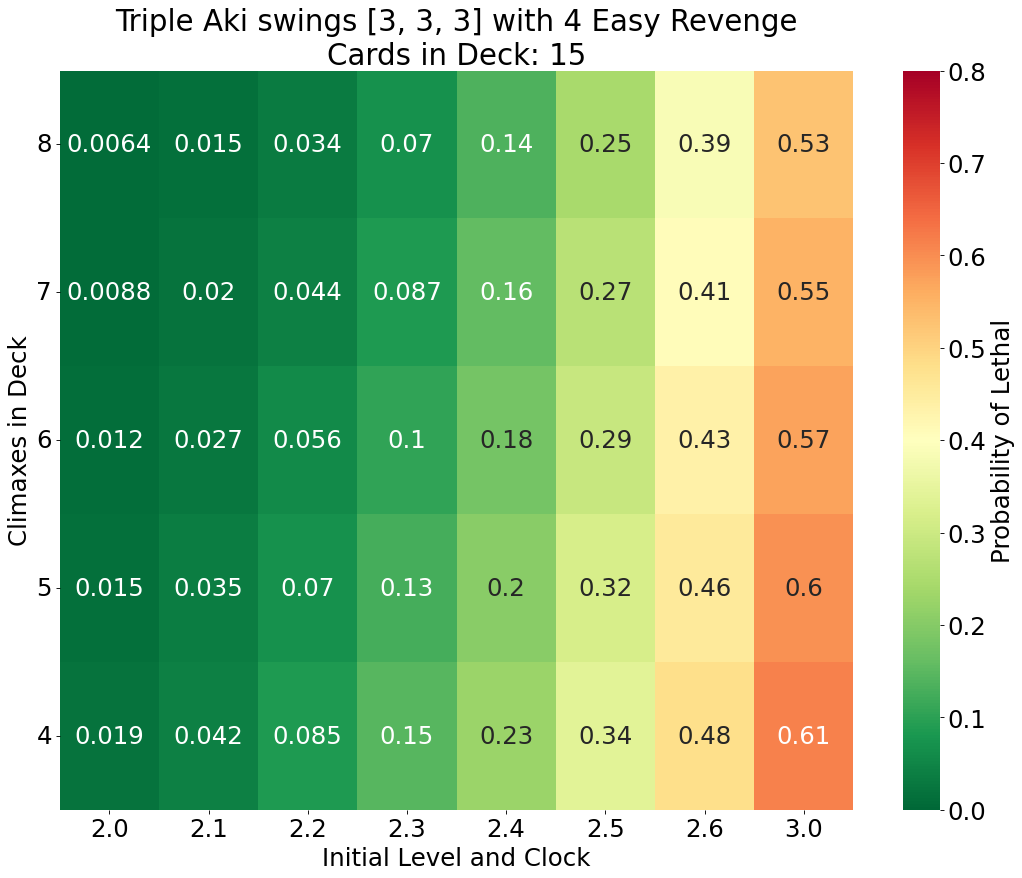
The probability of dealing lethal damage decreases between 1.4%-14.2% and by 9% on average across these gamestates when compared to Scenario 1B. Compressing is indeed a valid strategy for minimizing damage even against Aki. However, it’s worth noting that Aki still has above a fifty percent chance of killing a player from 3.0 even with an absurd compression of 8-in-15. While I have not calculated the odds of other finishers sticking lethal damage, I can think of none that could retain such high odds in compressed gamestates. This is definitely a strong selling point of Aki.
Another strategy worth discussing is healing. In order to analyze the effect of healing within a scenario we need to assume that the resources used for healing (e.g. two stock) would have been spent in another manner if the player opted to not heal. In actual gameplay opting to not heal can conserve resources and improve compression. In Scenarios 1A-1C healing one point drops the odds between 0.9%-14.6% and by 8.3% on average. These values are comparable to the reductions seen when comparing Scenarios 1B and 1C. Please keep in mind that these scenarios reflect compression based on how well Aki’s opponent has been able to build up their resources. In practice it is often not possible for a player to transition from the same grid square between these scenarios in a single turn. An analysis of the tradeoff between practical compression actions vs healing could be a future article.
Scenarios 2A and 2B - How much does Easy Revenge matter?
Everyone knows that the Easy Revenge event is important for Aki’s combo, but we were curious how much does each copy of the event impact the odds? In Scenarios 2A and 2B, we repeat Scenario 1B where Aki’s opponent has 20 cards in their deck, but we consider that the Aki player was only able to get three or two copies of Easy Revenge into memory respectively.
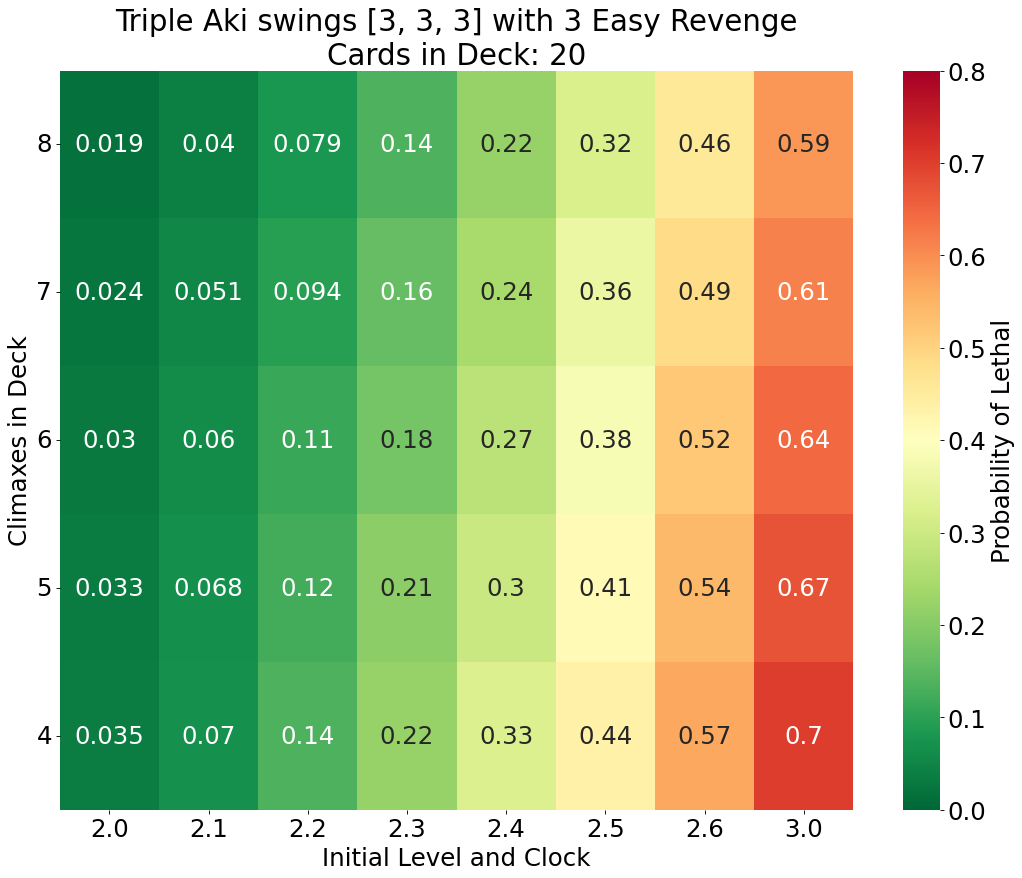
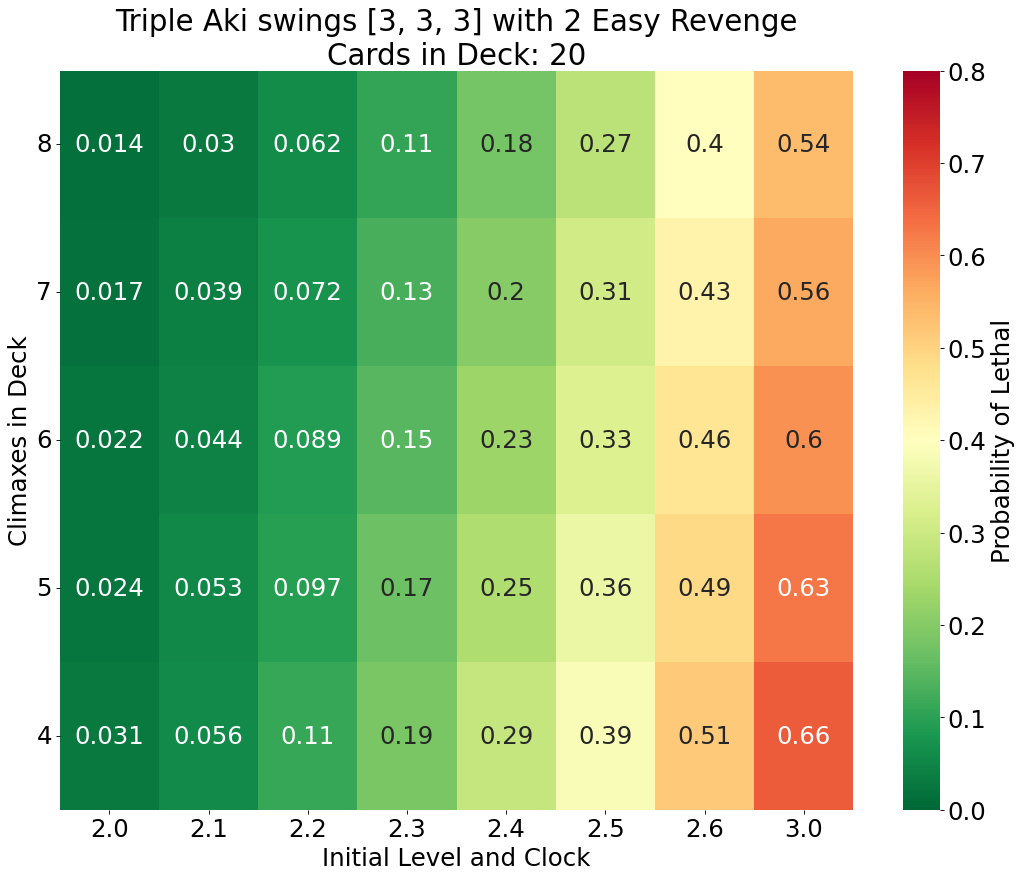
Naturally we observe that the probability of hitting the opponent to level 4 decreases as the number of Easy Revenge events decrease. On average the third copy of the event increases the odds by 3.4% and the fourth copy increases the odds by 2.7%.
Scenarios 3A, 3B, and 3C - How much does the third Aki matter?
Aki’s on play ability to salvage a character from the waiting room makes it much easier for the Aki player to field three copies for the finishing combo. But there are concerns that Aki could be limited to two copies on the next English restriction list update, mirroring the Japanese Weiss restrictions. [This might be the only part of this article relevant after the July 11th announcement stream. I really wish I was able to complete this blog post sooner.1] Hence we are concerned how effective are two copies of Aki with combo followed by a vanilla attack? Scenarios 3A-3C mirror Scenarios 1A-1C but for double Aki instead of triple.
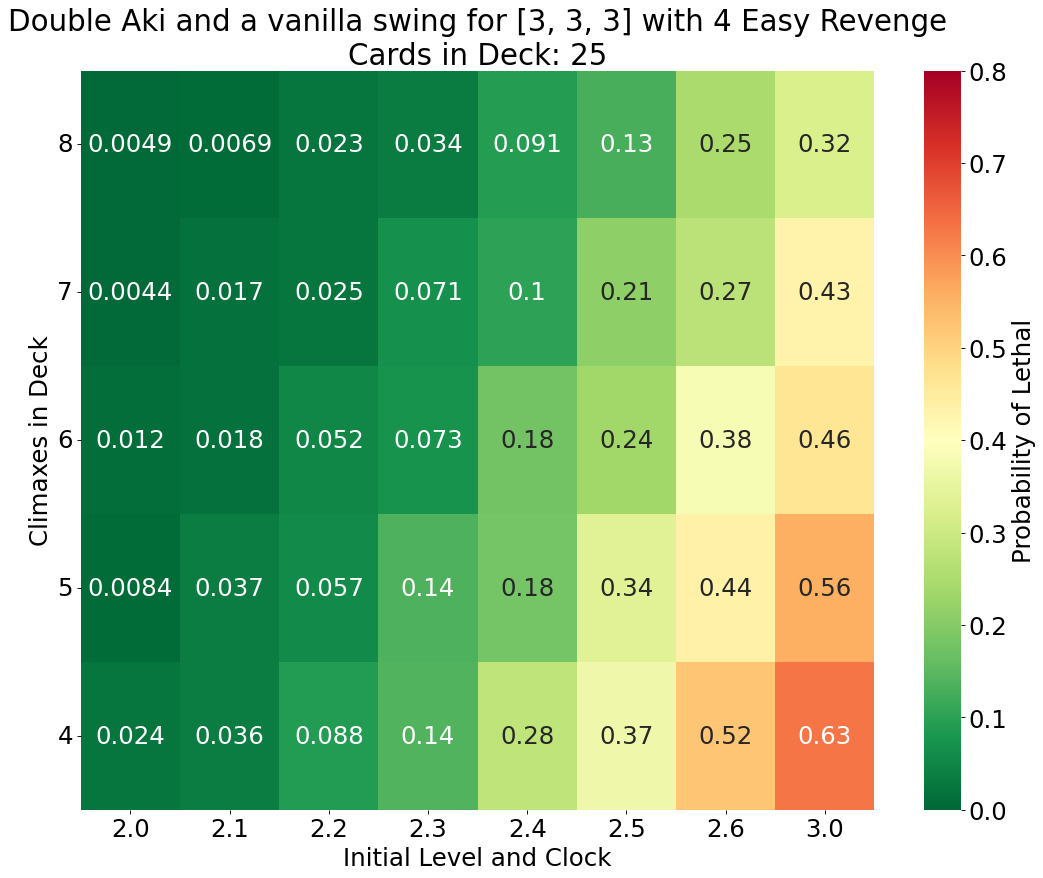
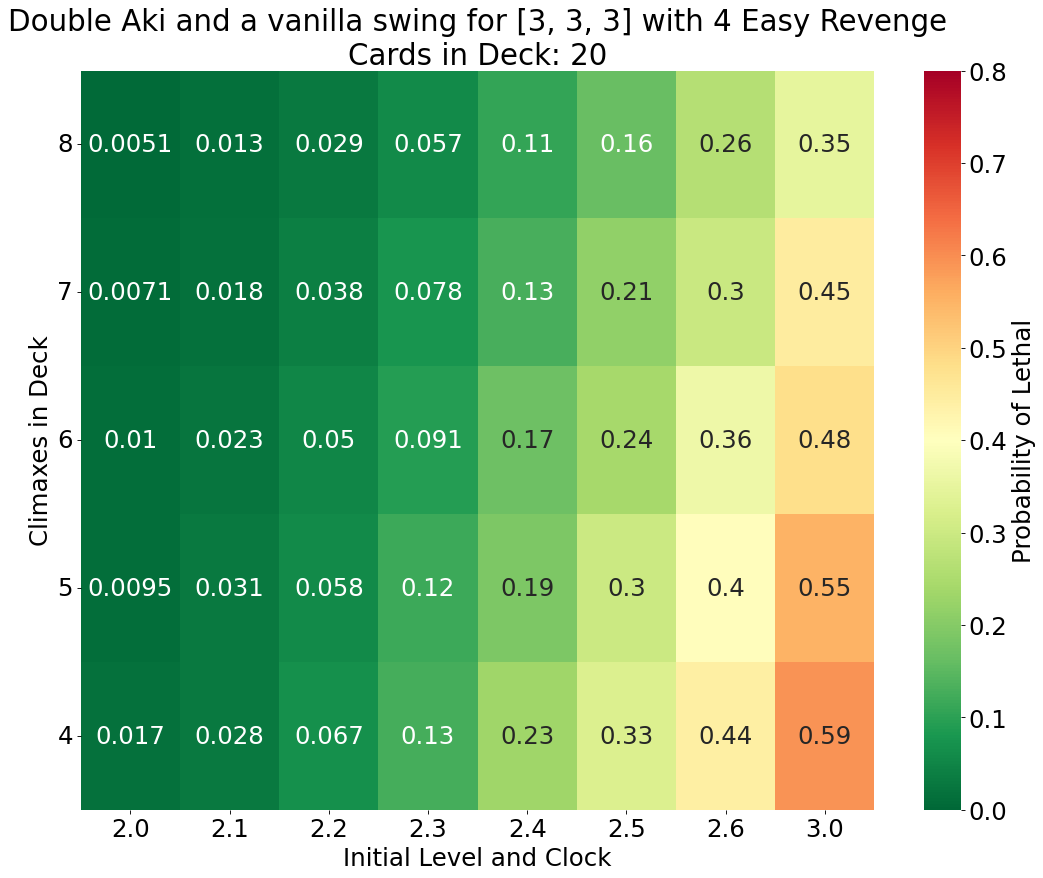
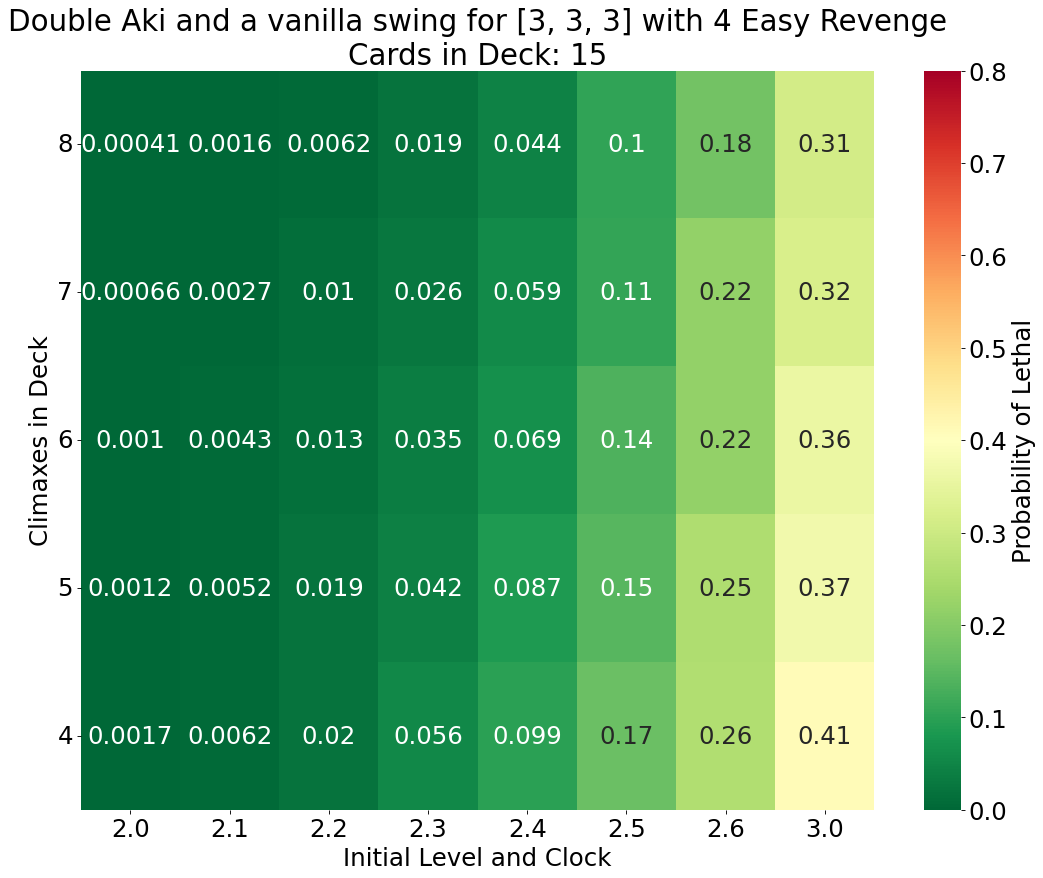
The odds of Aki’s victory noticeably drop without the third copy. On average the third Aki adds 15%, 12%, and 11% when the opponent has 25, 20, and 15 cards in their deck respectively. It is worth noting that for the cases where there are 7 or 8 climaxes in the deck double Aki has better odds (by no more than 3%) when the deck has 20 cards compared to 25 cards. This is a rare case of compression working in Aki’s favor, as the odds then decline for the 15 card deck scenario.
Conclusion: Please don’t hit yourself to level 3 unnecessarily or ‘tactically decompress’
In 2024 Weiss, finishers are more effective than ever and many players will opt to push themselves to level 3 believing there is no hope to survive at mid to late level 2. In the face of one of the greatest threats, “Public Safety Devil Extermination Special Division 4, Aki Hayakawa,” we seek to understand if there is hope to survive and how to minimize the odds.
To compute the odds of Aki defeating a player we constructed a tree of resulting gamestates with a layer of nodes for each action during the attack phase. We used greedy logic to determine Aki’s on attack effect sequencing. We varied the parameters of the root or initial gamestate to observe how the odds change with respect to these parameters. A notable takeaway is busting the myth of the ‘tactical decompress.’ Having more climaxes and less non-climaxes in the deck generally decreases the odds of death. However, it is worth noting that Aki’s odds are still respectable in many compressed scenarios. While we have not calculated the odds of other finishers we can imagine few that would fare this well. The other means of reducing lethal odds is healing. In our scenarios we observed the effect of healing was comparable to the benefit of compression by means of resources.
Besides adjusting the parameters of the opponent’s deck, we also tweaked the parameters of the Aki player. We observed that each copy of the Easy Revenge event contributed close to 3%. We also observed that the 3rd copy of Aki adds 11%-15% to lethal over only double Aki combo. You may want to keep these stats in mind should the next English restriction list mirror the Japanese one.
In actual gameplay, as Aki’s opponent you will need to weigh your options at late level 2 between healing, compressing, and pushing yourself to level 3 to perform your finishing combo first. The best choice will depend on your gamestate and resources available (as well as the Aki player’s). There will be times when healing or compressing will give better odds than pushing yourself to 3.0 and vice versa. We hope that probabilities presented in this article help you make informed choices in gameplay.
Appendix A: When Greedy Aki isn’t optimal
There are edge cases where trying to maximize the damage may not be the optimal play. One such case is when Aki’s opponent is at 3.3 with a 7 card deck with 0 climaxes and the Aki player has 4 Easy Revenge in memory, a blank trigger on top of their deck, and one Aki attack remaining. The greedy play is for Aki to use all four Easy Revenge effects to mill the bottom four cards of the opponent’s deck, which creates a possibility for the icy tail to hit a climax on the next deck. But this also removes the certainty of Aki’s attack damage connecting and winning the game. If the opponent is at 3.2 then this greedy play is necessary to have a chance at victory.
Appendix B: Results Tables
Here we have the results generated from the scenarios in Part 3 presented in tables. In addition to the parameters and lethal probability, we have also included the runtime of our script for curious readers.
Excel sheet of results here: Aki Tables
Footnote:
- Well, at least it'll be here for next year's no bans tournament -Ben